SheardLab.org | Research

Gallery

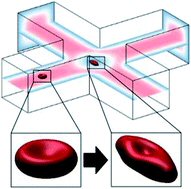
Simulations reveal the connection between the deformation of cells in mirco-fluidic systems, and applied stress.
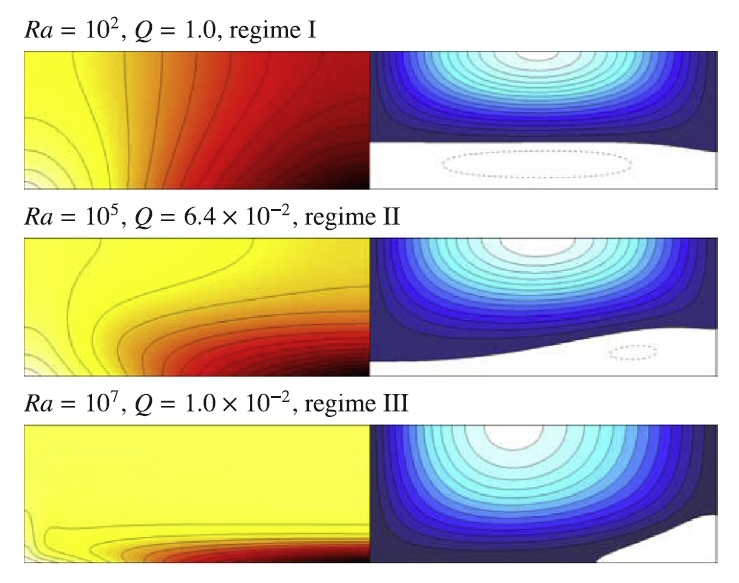
Suppression of radial horizontal convection in a rotating system with increasing rotation rate.
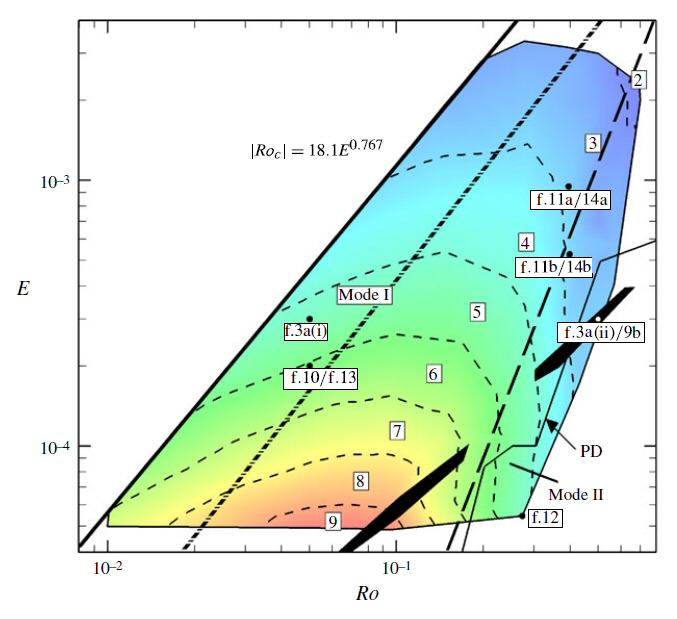
The first linear stability analysis of Stewartson layers in a differential-rotation system.
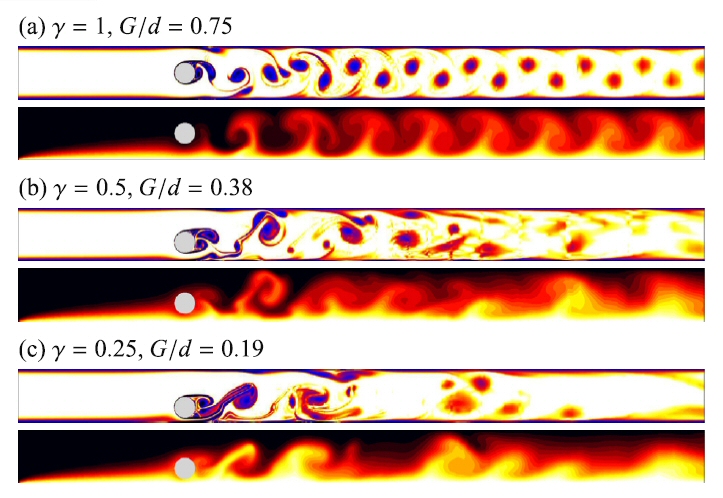
Heat transfer in quasi-2D MHD duct flows maximised by placing a turbulence generator approximately one diameter from a hot side-wall.
Numerical simulation providing insight into the shear environment around idealised thrombus obstacles in micro-flows.
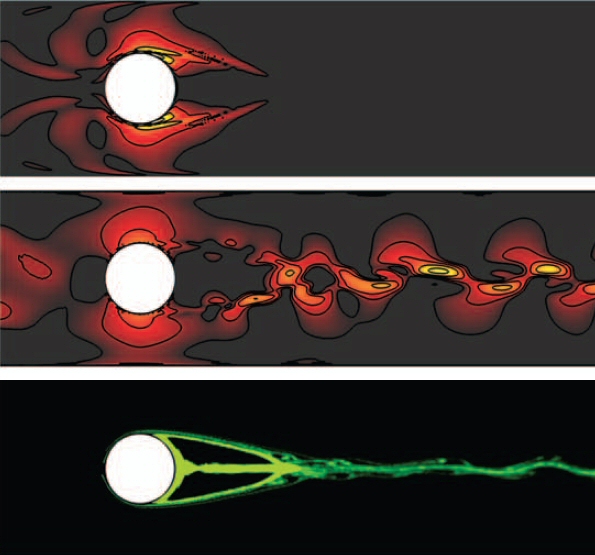
Transient growth analysis reveals sensitive regions in the flow past tubulence promotors in duct flows.
High-resolution simulations capture the destruction of a smaller vortex proximate to a stronger vortex.
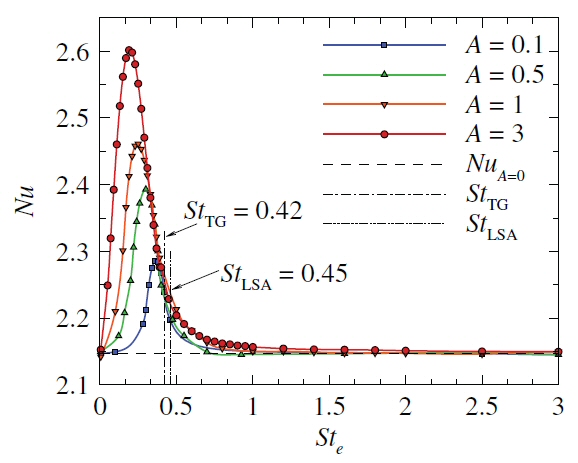
Active forcing via torsional oscillation of a turbulence promoter enhances heat transfer in an MHD duct flow.
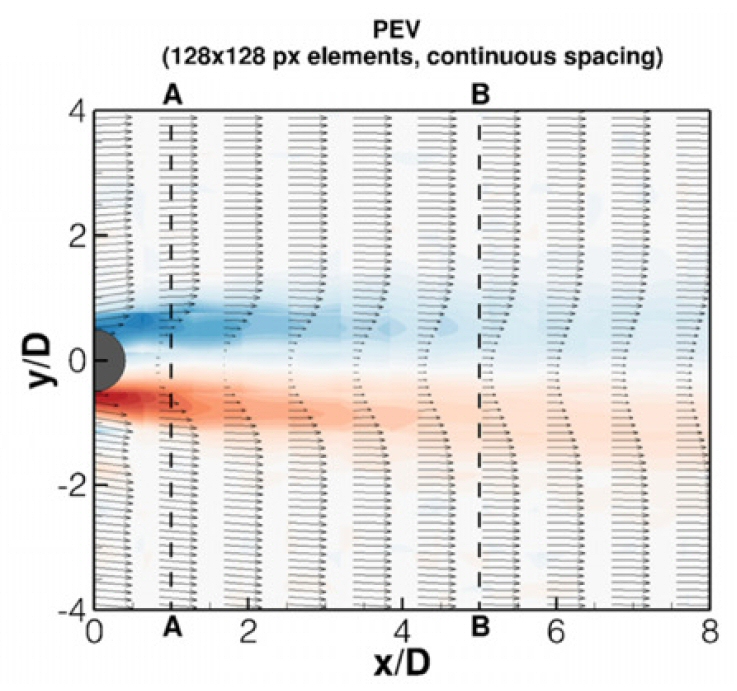
An award-winning processing technique enhances the quality of particle image velocimetry (PIV) measurements.
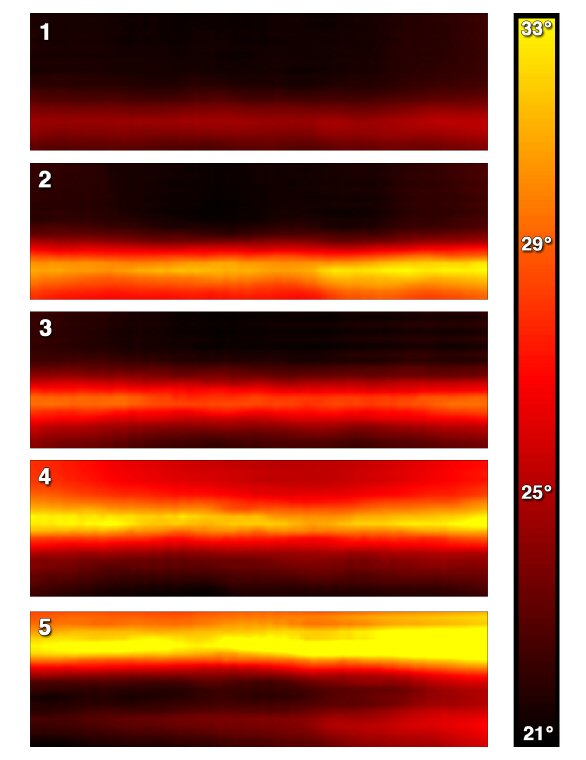
A buoyant plume rises from a hot-wire, captured using an image processing techniqe exploiting refractive-index changes in the fluid.
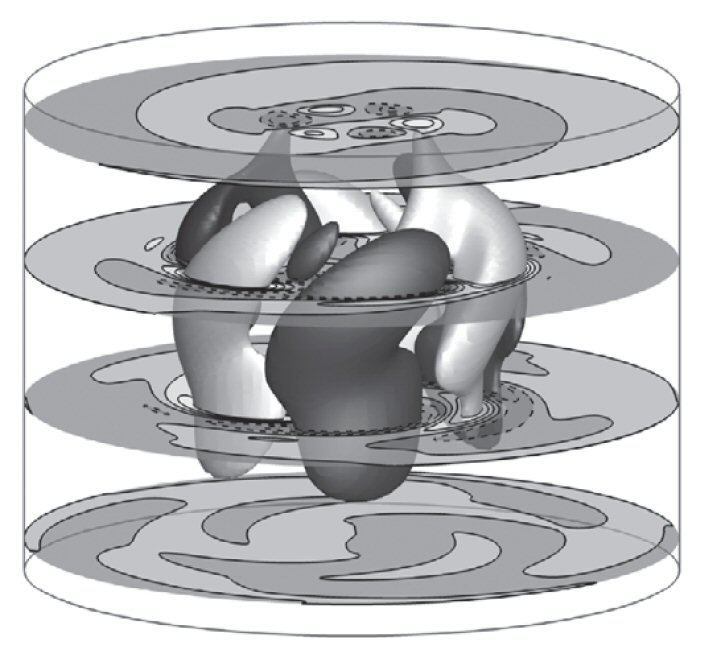
Instability structures emerge around a vortex breakdown bubble in a free-surface stirred-flask bioreactor model.
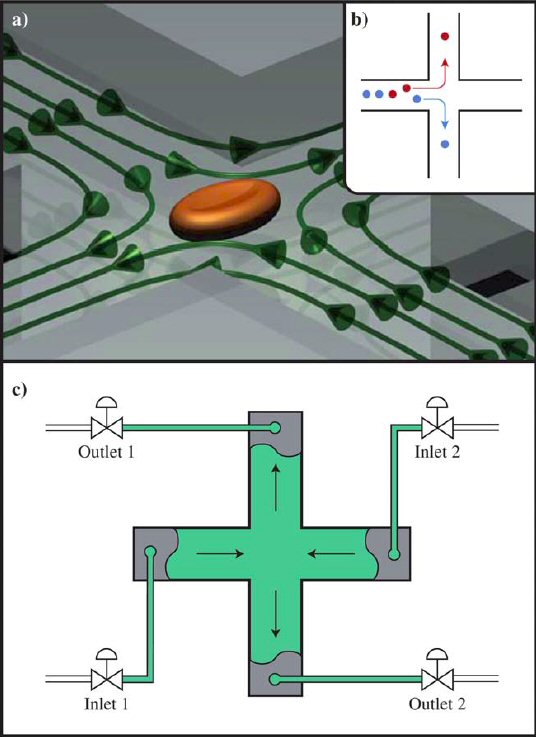
A micro-fluidic lab-on-a-chip system for capturing, measuring and sorting particles and cells is synthesized.
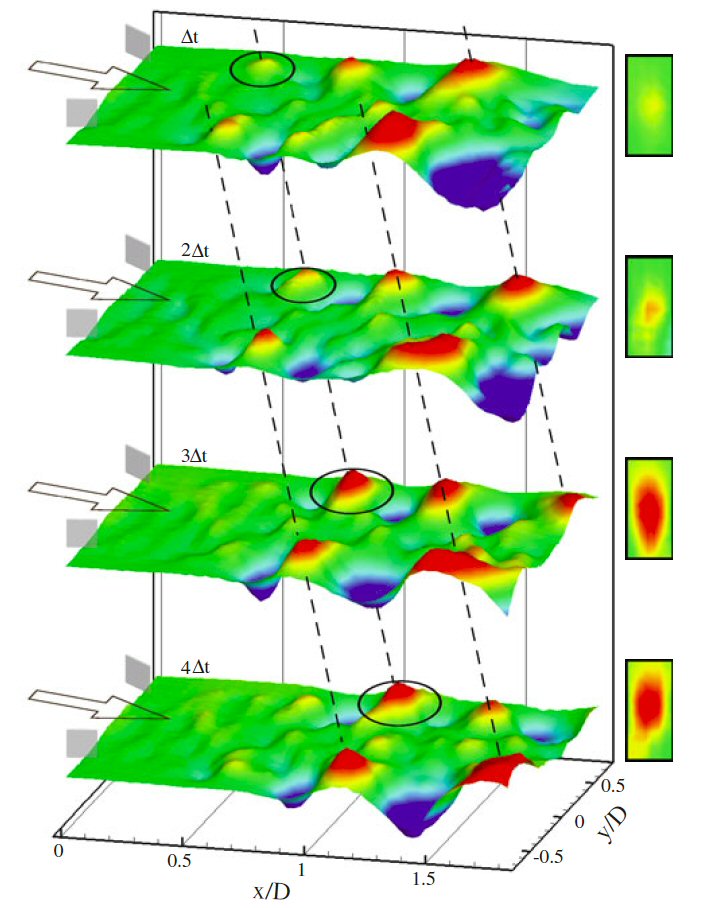
Our PIV topography measurement technique is employed to study wave structures in supersonic jets through the hydraulic analogy.
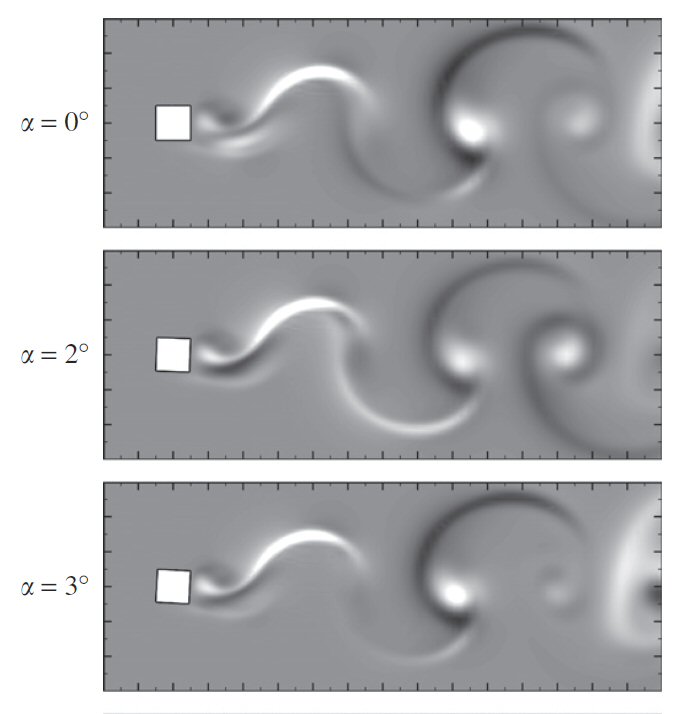
Careful analysis reveals subtle feaetures of the three-dimensional stability of wakes with subtle changes in symmetry of the flow.
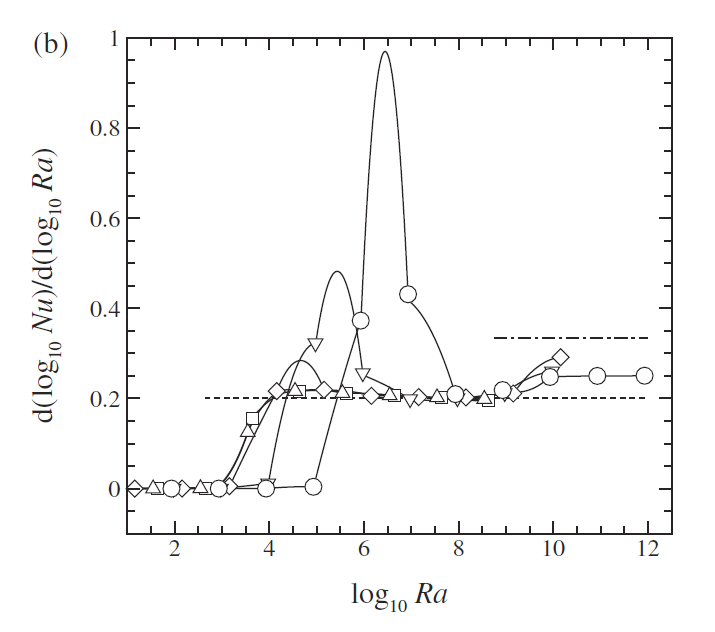
Evidence that instability in the forcing boundary layer in horizontal convection flows leads to an elevation of the power-law scaling between Nusselt number and Rayleigh number is revealed.
Linear stability analysis reveals three-dimensional instability modes for unequal counter-rotating vortex pairs.
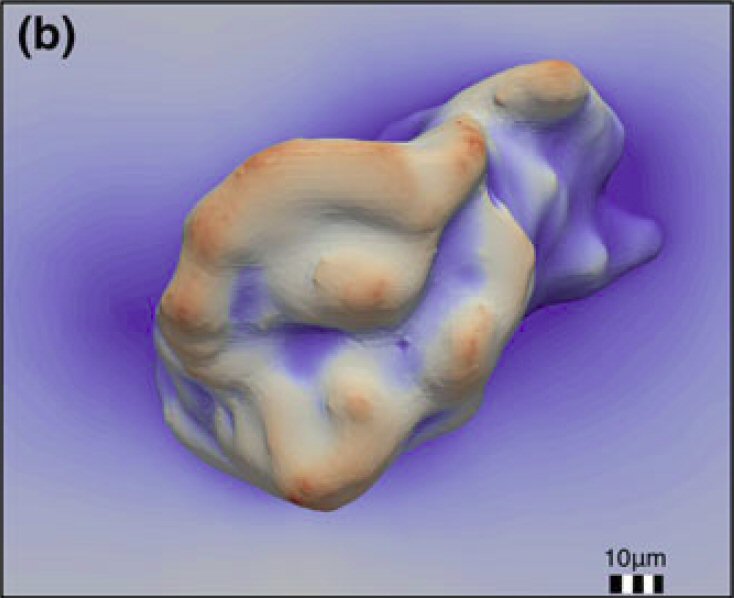
A computation of the surface shear on a digitized model of an actual thrombotic plaque grown in vitro.
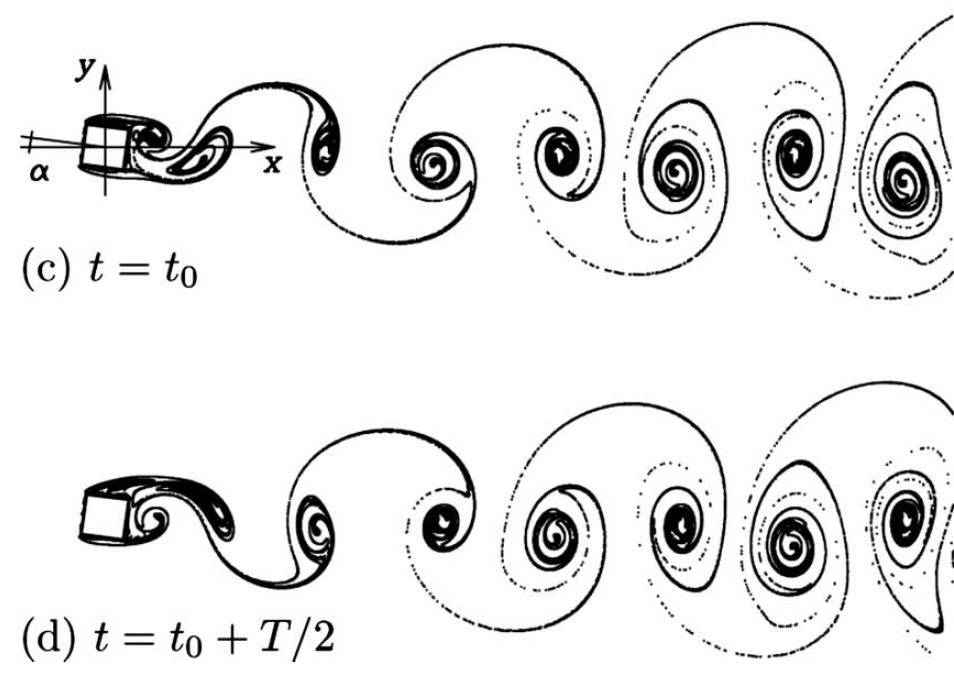
For the first time, the threshold between quasi-periodic and subharmonic wake instabilities is found to occur after a finite loss of wake symmetry.
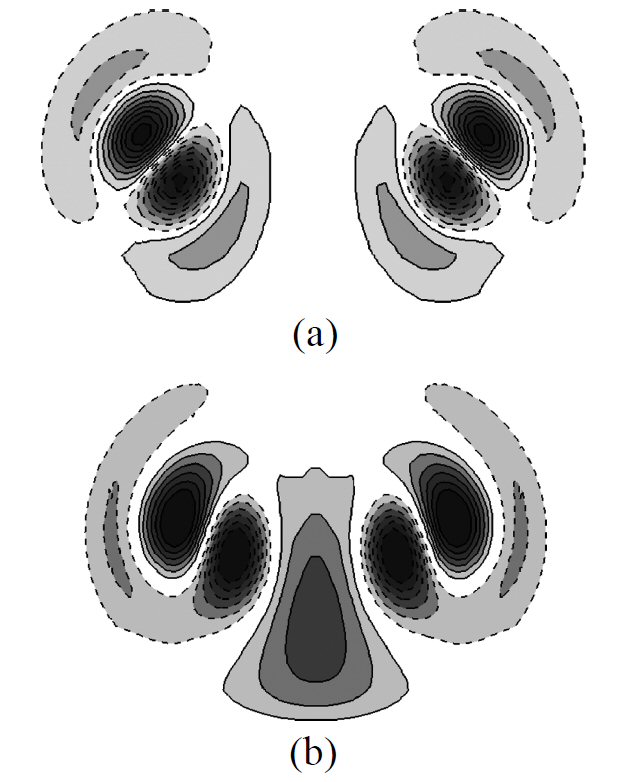
Linear stability analysis finds stark differences in three-dimensional mode shapes when a counter-rotating vortex pair is brought closer together.
A high-frequency vibration invokes a swirl mixing mechanism at T-junections in micro-fluidic systems.
Award-winning visualization of shock-cell structures in an hydraulic analogy of a supersonic nozzle flow using our imaging-based topography measurement method.
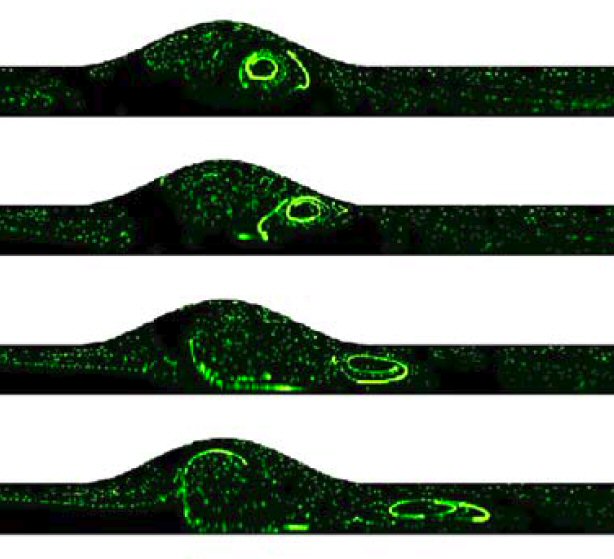
An invited contribution to a Special Issue volume reveals detailed dynamics of flows through fusiform aortic aneurysm geometries.
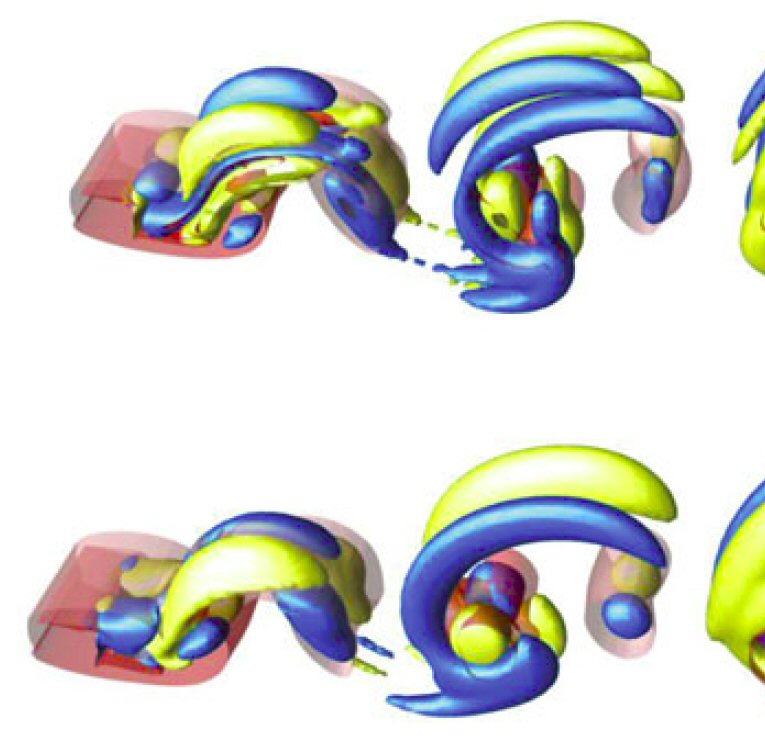
Three-dimensional instabilities in the wakes behind obstacles with square cross-sections aligned at various angles to the oncoming flow are uncovered.
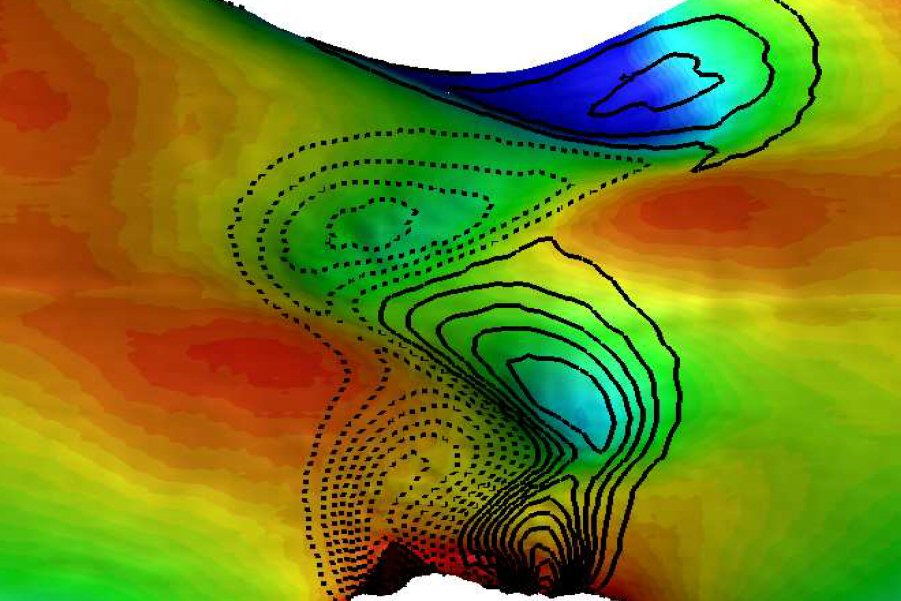
A new imaging-based method captures free-surface deformation caused by wake vortices behind a cylinder.
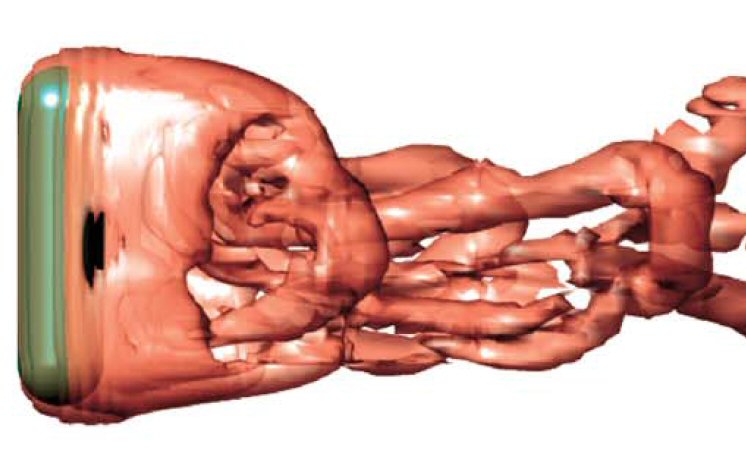
Revealing the behaviour of flow past obstacles ranging from spheres to circular cylinders.
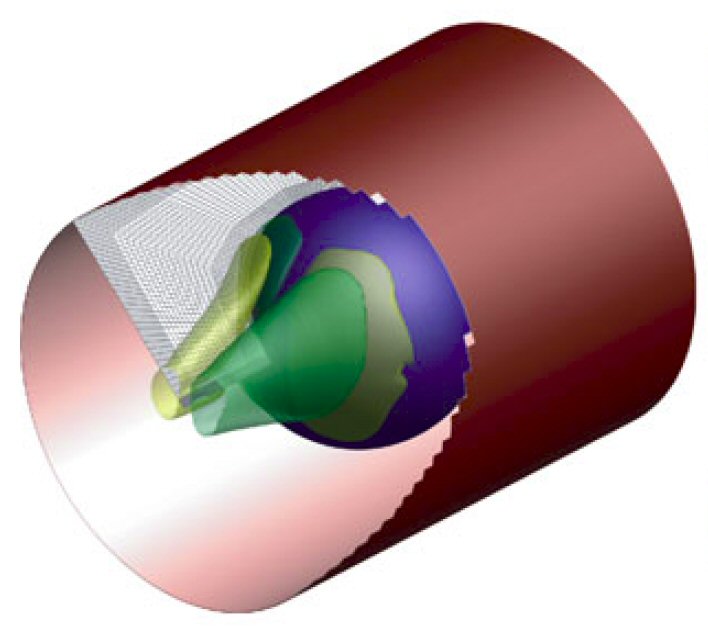
The velocity of particles carried in a tube is found to be proportional to the imposed pressure gradient.
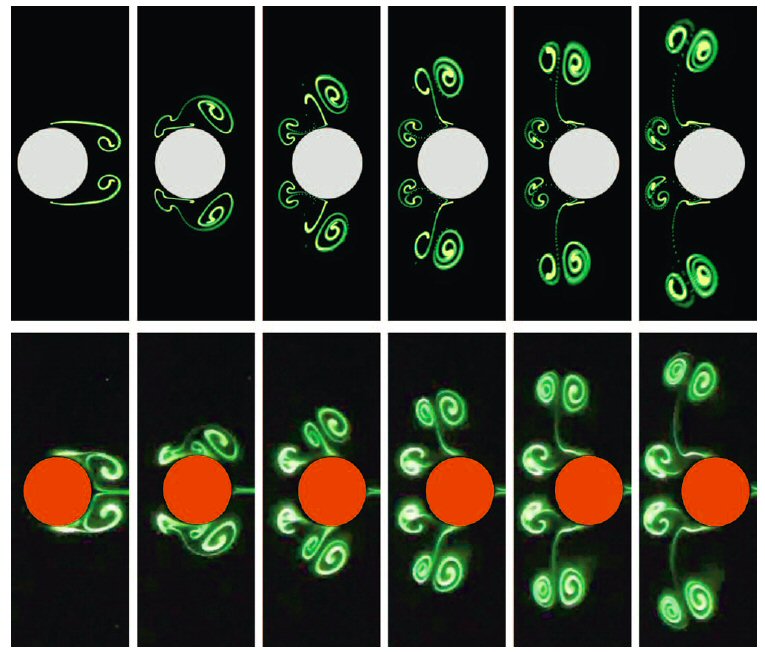
Combining laboratory and numerical experiments to reveal the kinematics of the flow around a body brought to a sudden stop.
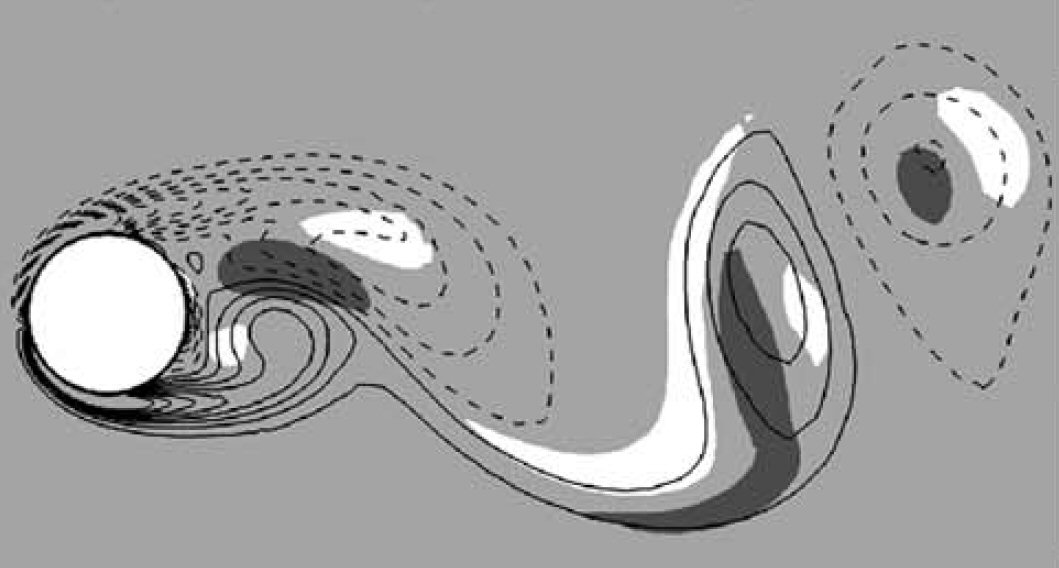
We report the first side-by-side comparison of the time-periodic linear instability modes seeding the well-known Mode A and B instabilities and the subharmonic Mode C instability.
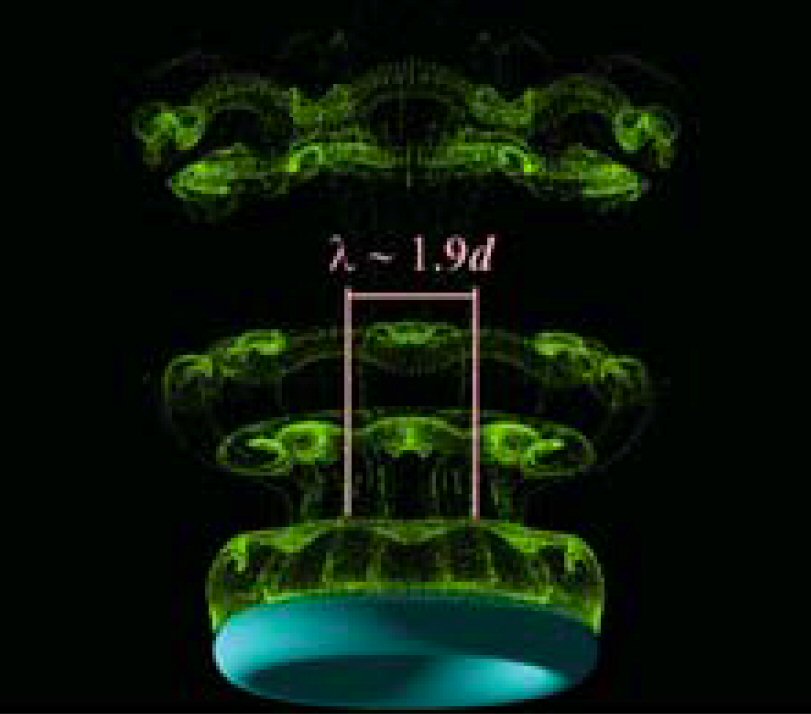
In collaboration with Dr Thomas Leweke, IRPHE, France, we are the first to capture the subharmonic Mode C instability in the laboratory.
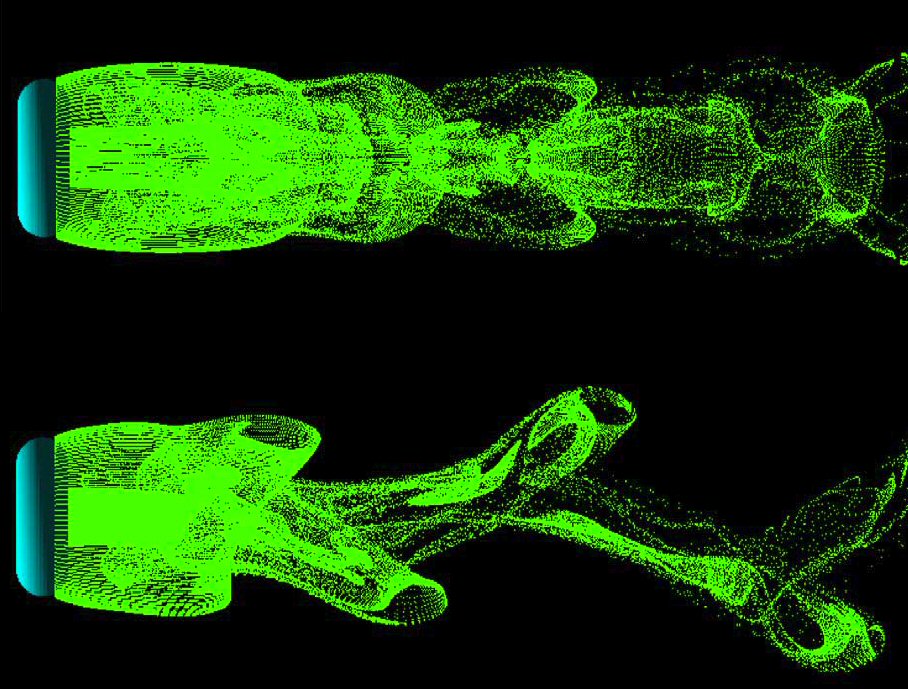
Revealing similarities and differences in the flow past solid and open obstacles.
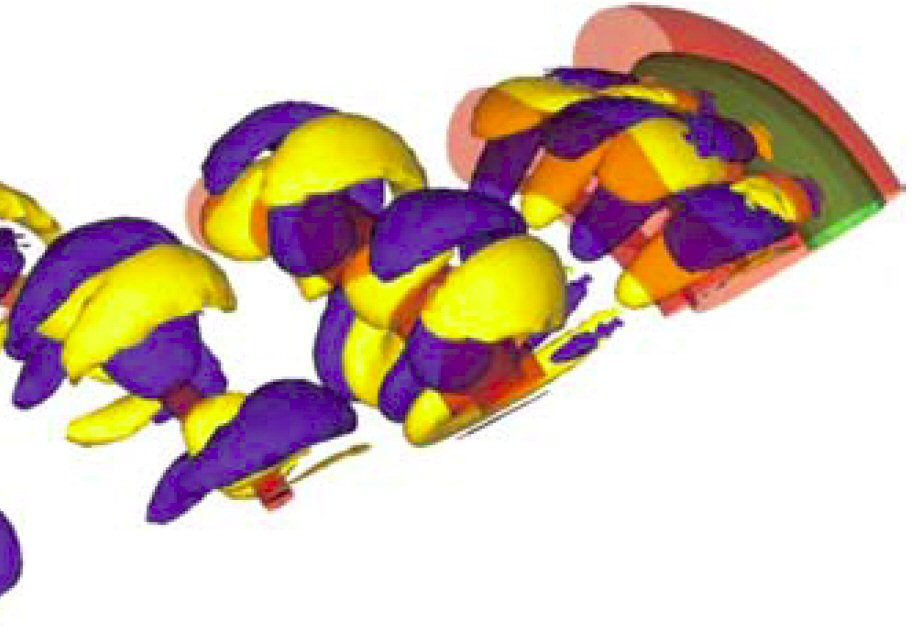
Capturing Mode C: The first direct numerical simulation of a subarmonic three-dimensional instability in a bluff body wake, originally predicted by our landmark linear stability analysis.
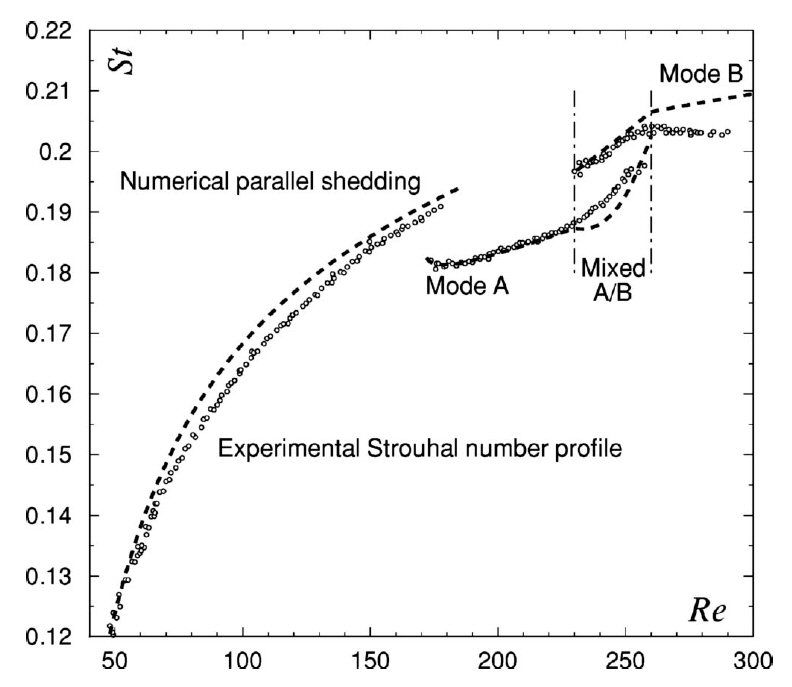
Our coupled Landau model (dashed line) reproducing experimental measurements of the shedding frequency behind a circular cylinder through both the two-dimensional regime and the inception of three-dimensional instability modes.